Key derivation and usage#
Concordium employs a SLIP-10/BIP32 hierarchial key derivation scheme to generate all cryptographic key material required for account creation and operation on the blockchain.
Each account is associated with an Identity Credential issued to the user by an Identity Provider (IDP). This structure is reflected in the key derivation tree structure:
Each Identity Provider has its own subtree
Within each IDP subtree, there are individual subtrees for each Identity Credential issued to the user
The subtree of a single Identity Credential consists of:
A subtree dedicated to account signature keys used to sign transfers
Multiple subtrees that generate cryptographic material for the ID object itself
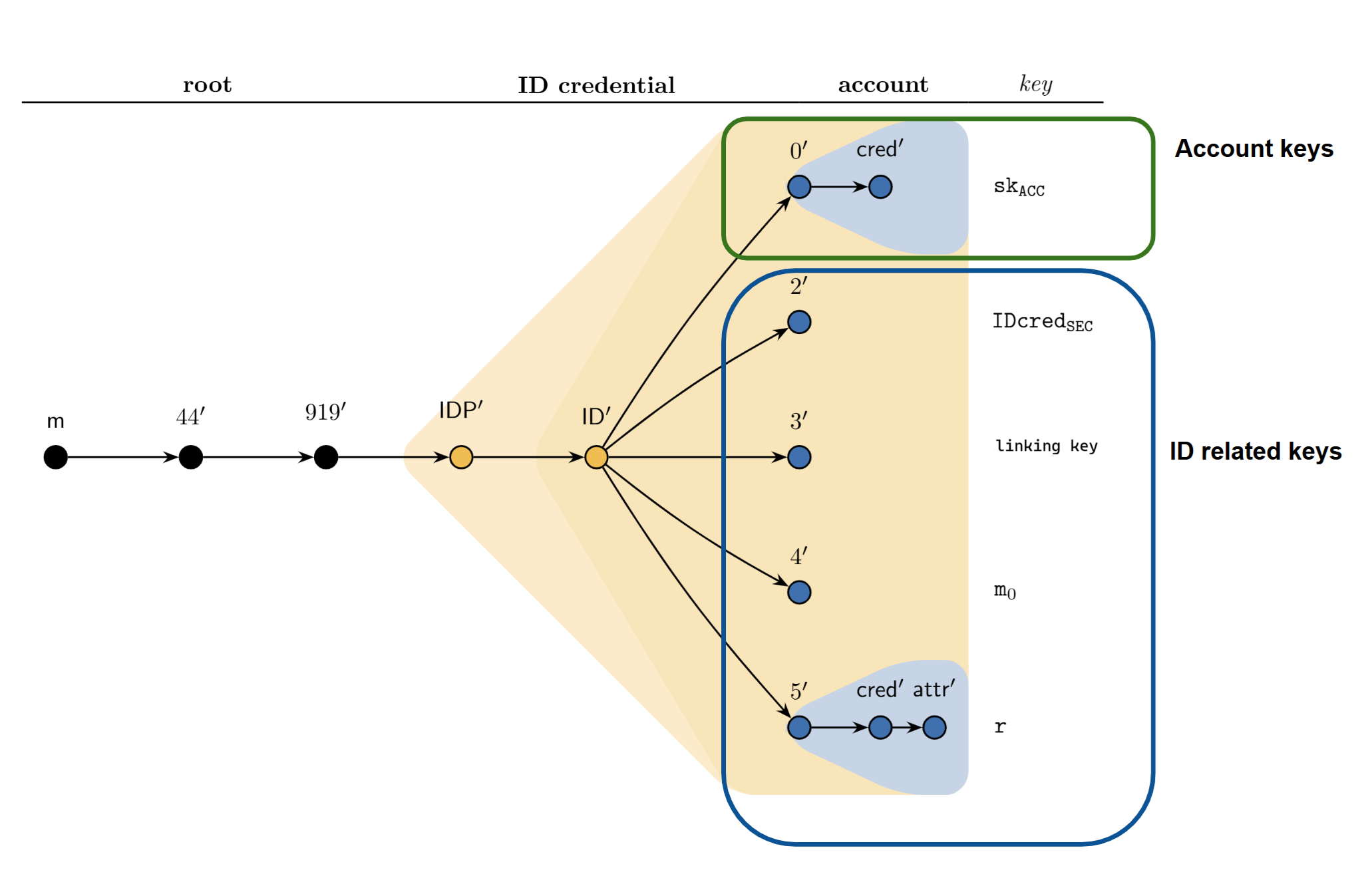
Derivation structure#
All cryptographic keys related to an identity object and the related accounts are generated from a subtree with prefix=m/44’/919’/IDP’/ID’ where IDP is the index of the Identity Provider and ID is the index of the ID, e.g. ID=0 for the first identity issued to the user.
Account keys#
Subtree 0’ is used to derive signature keys for accounts related to the ID objects. That is, prefix/0’/cred’ is the key for the account with index cred’ (starting at 0).
Holder Identifier#
Subtree 2’ defines the holder identifier (essentially a public/private key pair) which is used as a user identifier in Concordium’s Identity Disclosure scheme. Technically, the public identifier IDcredPub is an element in G1 of BLS12-381 and the secret identifier IDcredSec is a field element in the corresponding finite field.
Each account created with the given identity contains the public identifier in encrypted form (technically, secret shared where each share is ElGamal encrypted under the public key of a Privacy Guardian (PG). Generating the encryption requires knowledge of the secret identifier. The correctness of this encryption is proven in zero-knowledge as part of a larger Zero-knowledge proof for the account opening. The proof is a combination of Bulletproofs and Sigma protocols over BLS12-381. For generating the zero-knowledge proof, one needs the secret identifier.
Pseudo-random function Key#
Subtree 3’ defines the PRF key used to generate the addresses of accounts. Technically the account address is PRF(PRF key, x) where x is the account index. Knowing the PRF key allows identifying all accounts that have been generated from a given identity.
When an identity is issued, the Identity Provider will store an encrypted copy of the PRF key (same encryption scheme as mentioned above for the holder identifier). The correctness of this encryption is proven to the Identity Provider in zero-knowledge. The proof is again a combination of Bulletproofs and Sigma protocols over BLS12-381.
Furthermore, in the account opening proof one also needs to prove that the account address was correctly computed. This also requires knowledge of the PRF key.
Blind signature randomness#
Subtree 4’ defines randomness m0 used in a blind signature protocol between the Identity Provider and the user when issuing a new identity. This allows the user to get a signature on both the identity attributes (e.g. name, birthdate) and things like the PRF key and the IDcredSec without the Identity Provider learning the secret values.
The randomness m0 is needed as part of the ID issuance protocol. As part of this protocol the user needs to prove knowledge of m0. This is part of the same zero-knowledge proof as mentioned in the PRF key section.
We observe that the randomness could be generated from scratch by the wallet during the ID issuance process. However, by having it generated from the seed phrase, the user can recover the signature from the Identity Provider at a later point (without having to do another blind signing ceremony).
Pedersen commitment randomness#
Subtree 5’ defines the randomness (aka opening information) used in the Pedersen commitments that commit the account to the attributes of the identity. These commitments can be used to prove (ideally, off-chain) statements about the account holder.
The randomness in these commitments is used to prove statements about the account holder in zero-knowledge proofs.
As part of the account opening proof, the user also needs to show that the commitments have been generated correctly from the ID attributes signed by the Identity Provider. This again requires knowledge of the commit randomness.
The advantage of generating the commit randomness from the seed phrase is that the user can recover the commitment opening information.
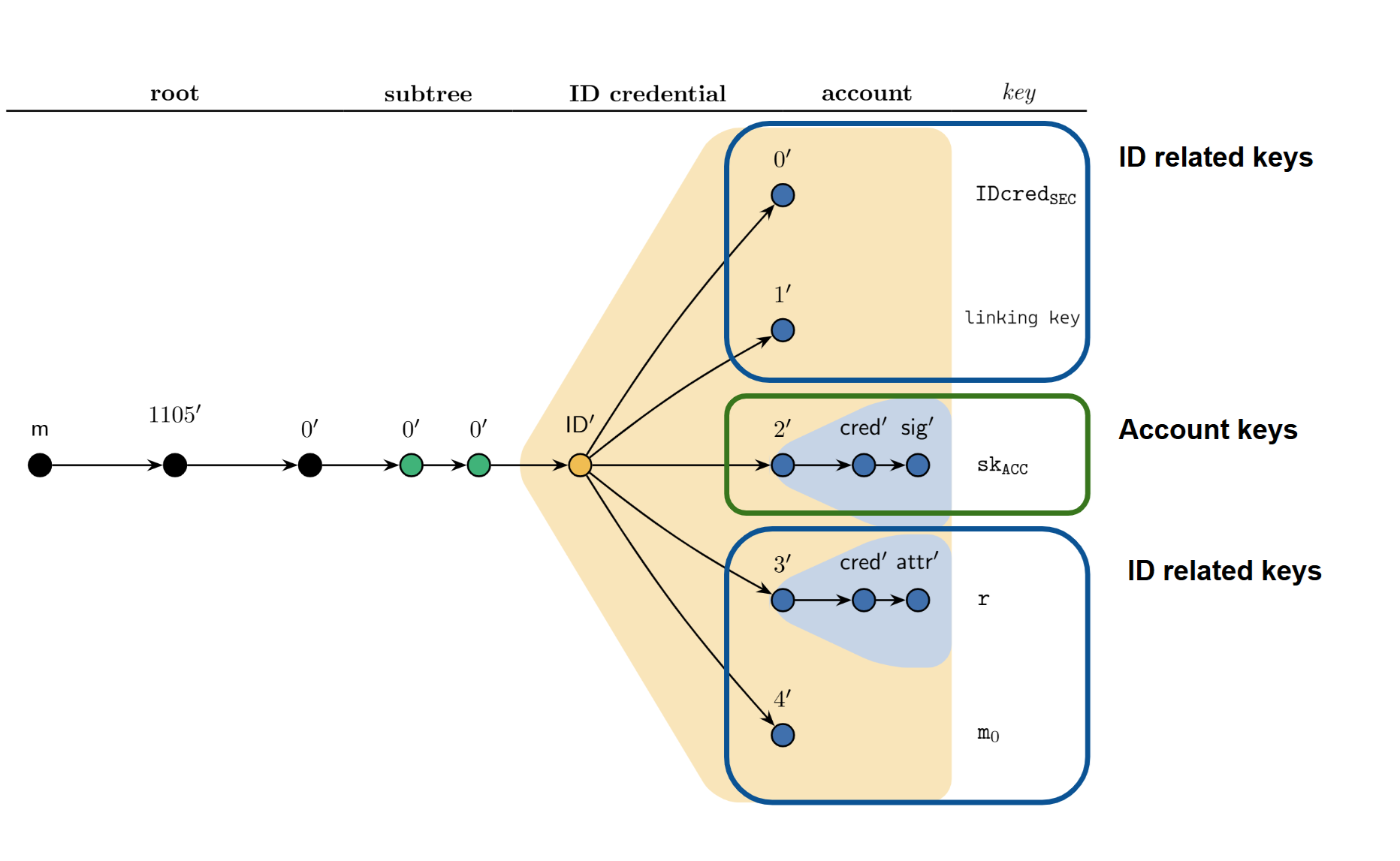
Legacy derivation tree#
Note
The legacy derivation tree is only mentioned here for completeness and should never be used for new products.
Some older wallets use a legacy derivation tree. The only differences between this and the derivation tree described above are the prefix m/1105’/0/0’/0’/ID’, which omits the Identity Provider index, and the use of different indices for the key subtrees in the Identity Credential subtree. For example, in the legacy tree the account signature keys are located in subtree 2’ instead of 0’. It is important to note that the split of keys into subtrees is equivalent to those in the above tree.
